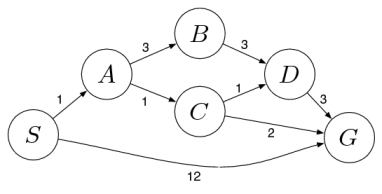
We will try to improve the efficiency of the Uniform Cost Search algorithm by using heuristics which we discussed in the previous post. By improving the efficiency I mean that the algorithm will expand less of the search tree and will give the optimal result faster. We start with the same search problem and search tree that we used for Uniform Cost Search. If you don’t know what search problems are or how search trees are created, visit this post.
A* Search Algorithm
We saw that Uniform Cost Search was optimal in terms of cost for a weighted graph. Now our aim will be to improve the efficiency of the algorithm with the help of heuristics. If you don’t know what heuristics are, visit this post. Particularly, we will be using admissible heuristics for A* Search.
A* Search also makes use of a priority queue just like Uniform Cost Search with the element stored being the path from the start state to a particular node, but the priority of an element is not the same. In Uniform Cost Search we used the actual cost of getting to a particular node from the start state as the priority. For A*, we use the cost of getting to a node plus the heuristic at that point as the priority. Let n be a particular node, then we define g(n) as the cost of getting to the node from the start state and h(n) as the heuristic at that node. The priority thus is f(n) = g(n) + h(n). The priority is maximum when the f(n) value is least. We use this priority queue in the following algorithm, which is quite similar to the Uniform Cost Search algorithm:
Insert the root node into the queue
While the queue is not empty
Dequeue the element with the highest priority
(If priorities are same, alphabetically smaller path is chosen)
If the path is ending in the goal state, print the path and exit
Else
Insert all the children of the dequeued element, with f(n) as the priority
While the queue is not empty
Dequeue the element with the highest priority
(If priorities are same, alphabetically smaller path is chosen)
If the path is ending in the goal state, print the path and exit
Else
Insert all the children of the dequeued element, with f(n) as the priority
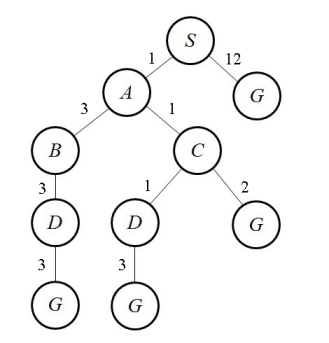
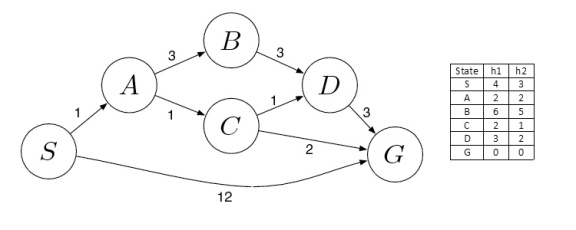
Now let us apply the algorithm on the above search tree and see what it gives us. We will go through each iteration and look at the final output. Each element of the priority queue is written as [path,f(n)]. We will use h1 as the heuristic, given in the diagram below.
Initialization: { [ S , 4 ] }
Iteration1: { [ S->A , 3 ] , [ S->G , 12 ] }
Iteration2: { [ S->A->C , 4 ] , [ S->A->B , 10 ] , [ S->G , 12 ] }
Iteration3: { [ S->A->C->G , 4 ] , [ S->A->C->D , 6 ] , [ S->A->B , 10 ] , [ S->G , 12] }
Iteration4 gives the final output as S->A->C->G.
Iteration1: { [ S->A , 3 ] , [ S->G , 12 ] }
Iteration2: { [ S->A->C , 4 ] , [ S->A->B , 10 ] , [ S->G , 12 ] }
Iteration3: { [ S->A->C->G , 4 ] , [ S->A->C->D , 6 ] , [ S->A->B , 10 ] , [ S->G , 12] }
Iteration4 gives the final output as S->A->C->G.
Things worth mentioning:
->The creation of the tree is not a part of the algorithm. It is just for visualization.
->The algorithm returns the first path encountered. It does not search for all paths.
->The algorithm returns a path which is optimal in terms of cost, if an admissible heuristic is used(this can be proved).
->The algorithm returns the first path encountered. It does not search for all paths.
->The algorithm returns a path which is optimal in terms of cost, if an admissible heuristic is used(this can be proved).
The above example illustrates that A* Search gives the optimal path faster than Uniform Cost Search. This is, however, true only if the heuristic is admissible. In general, the efficiency of the algorithm depends on the quality of the heuristic. The nearer the heuristic is to the actual cost, the better is the speed of the algorithm. Trivially, the heuristic can be taken to be 0, which gives the Uniform Cost Search algorithm.
